前言
2023年新高考一卷的立体几何“包含”问题在沉寂多月(其实最近广东新南方联盟也考了,不过那个和23高考极其相似)后再次以全新的难度和思维水平在浙江湖丽衢二模中出现,并“创飞”了不少考生。
其实对于此类问题,分析临界情况,还是可以找到突破点的。
题目
已知正四面体 A-BCD 的棱长为 1 ,若棱长为 a 的正方体能整体放入正四面体 A-BCD 中,则实数 a 的最大值为___________________.
典型错解
一个典型的错误是求四面体内接球半径并以它为正方体对角线。这样求出来的只是可以任意转动(限制在内接球内)的正方体棱长的最大值,而正方体棱长取到题目要求的最大值时,其应该是被完全“卡死”的。
题目分析
不难得出正四面体高为 \frac{\sqrt6}3
正方体棱长为 a ,则棱长最大时的临界情况就是上底面内接于截面正三角形。(通过平面几何容易证明,内接于三角形的最大正方形其中一条边与三角形底边重合,如图所示)
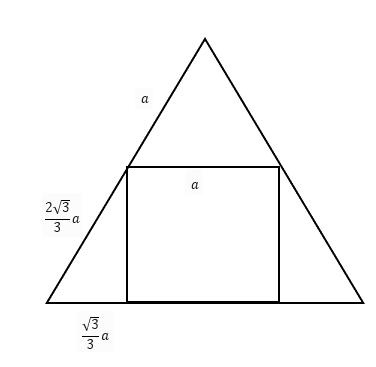
此时不难得出最小三角形的边长为 (\frac{2\sqrt3}{3}+1)a ,
再从竖直方向考虑,由于正四面体平行于底面截面边长与截面到底面的距离成线性关系(使用相似三角形易证明),当高度为 a 时,此时的边长应为 \frac{h-a}h=\frac{2-\sqrt6 a}2 ,联立两式,即解得 a=\frac6{4\sqrt3+6+3\sqrt6} .
容易证明,若 a 更大,则截面边长更小,不可能存在边长为 a 的内接正方形,故 a=\frac6{4\sqrt3+6+3\sqrt6} 即为最大.
思维过程
我们运用了“高度最大时的极限状况”得出临界值,并利用“高度”和“上底面”两个条件得出方程组解决问题。
最后,祝大家备考顺利!