一 换根DP简介
树形 DP 中的换根 DP 问题又被称为二次扫描,通常不会指定根结点,并且根结点的变化会对一些值,例如子结点深度和、点权和等产生影响。
通常需要两次 DFS,第一次 DFS 预处理诸如深度,点权和之类的信息,在第二次 DFS 开始运行换根动态规划。
二 相关例题
例题一
一. 题目传送门
题目来源
二. 解题思路
0. 前置说明
由题目描述不难看出,这是树形DP中的换根DP。
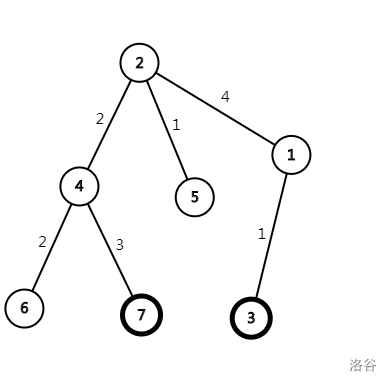
由样例 1 (形态如图 1 所示) 可知以 $i$ 为根时的最小代价为以 $i$ 为根的子树中从 $i$ 开始送人最后回到 $i$ 节点的路径减去 $i$ 的最长链的长度。

1. 相关约定
(1) $f(u)$ 为以 $u$ 为根的子树中从 $u$ 开始把所有家在 $u$ 的子树中的人送回家再返回 $u$ 节点的路程;
(2) $pos(u)$ 表示 $u$ 节点是不是某些人的家;
(3) $len(u)$ 表示以 $u$ 为起点向子树方向的最长链的长度, $slen(u)$ 表示以 $u$ 为起点向子树方向的次长链的长度;
(4) $g(u)$ 表示从 $u$ 开始把树上所有人送回家后再返回 $u$ 节点的最短路程.
(5) $maxson(u)$ 表示从$u$ 开始向子树方向的最长链所到达的第一个点
2. 换根DP流程
我们知道,换根DP要进行两次$DFS$, 第一次$DFS$ 收集该节点的子树的相关信息, 第二次$DFS$ 收集该节点至整棵树上的相关信息。
(1) 第一次$DFS$
我们利用 $pos(i)$ 来确定该点 $u$ 下有几个点 $i$ 是某些人的家,并用 $size(u)$ 来记录.
当 $size(u) \neq 0$ 时:
由定义 1 可知 $f(u) = \sum f(v) + 2 \times val(u, v)$,$v \in son(u)$ ,由定义 2 和定义 3 可知此时我们可以利用$v , v \in son(u)$ 来更新节点 $u$ 的 $len(u)$ 和 $slen(u)$ ;
即 $len(v) + val(v, u) \geq len(u)$ 时 $ slen(u) = len(u), len(u) = len(v) + val(v, u)$
$len(v) + val(v, u) \geq slen(u)$ 时 $ slen(u)= len(v) + val(v, u)$ .
(至于这个$slen(u)$ 的作用,后面再说)
(2) 第二次$DFS$
由定义 1 和定义 4 以及树的原始形态可知 $g(1) = f(1) $.
接下来我们利用第一次$DFS$得到的有关信息来得到 $g(u)$:
将图 1 稍作变换可得到图 2 ,此时 2 为树根.
我们发现此时$size(2) \neq 0$ ,并且$k - size(2) \neq 0$ ,由图容易得到(希望有$jvlao$能给出相关证明)$g(2) = g(1)$
不完全归纳可知:
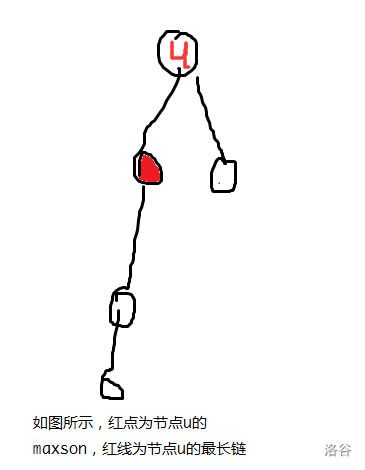
- 对于$ ∀v \in son(u)$ 并且 $size(v) \neq 0$ 并且 $k -size(v) \neq 0$ , 都有 $g(v) = g(u)$.
当$len(v) \leq len(u) + val(v, u)$ 并且 $v \neq maxson(u)$时,则可得 $len(v) = len(u) + val(v, u)$ , $maxson(v) = u$.
当$len(v) \leq len(u) + val(v, u)$ 并且 $v = maxson(u) $时,如果用 $u$ 的相关信息更新$len(v)$则会与定义(3)矛盾(此时不再是一条链了).
当$len(v) \leq slen(u) + val(v, u) $ 时,说明 $u$ 的次长链可以更新 $v$ 的最长链(由定义(3)可知此时不会出现向上面一样的情况),则可得 $len(v) = slen(u) + val(v, u)$ , $maxson(v) = u$.
当 $slen(v) \leq len(u) + val(v, u)$ 并且 $v \neq maxson(u)$ 时,说明 $u$ 的最长链可以更新 $v$ 的最长链.(式子仿照上面)
当 $slen(v) \leq len(u) + val(v, u)$ 并且 $v = maxson(u)$ 时,说明 $u$ 的最长链不可以更新 $v$ 的最长链(此时不再是一条链,与定义(4)矛盾).
当 $slen(v) \leq slen(u) + val(v, u)$ 时,说明 $u$ 的次长链可以更新 $v$ 的次长链.
- 对于$ ∀v \in son(u)$ 并且 $size(v) = 0$ 时,由定义(1)(3)(4)可知 $g(v) = g(u) + 2 \times val(v, u)$ , $len(v) = len(u) +val(v, u)$.
- 对于$ ∀v \in son(u)$ 并且 $size(v) \neq 0$ 并且 $k -size(v) =0$ 时,由定义(1)(4)以及题意可知$g(v) = f(v)$.
(3)注意事项
- 记得开 long long(三年OI一场空, 不开long long见祖宗).
- 由相关定义可知最后输出的是 $g(i) - len(i).$
三. 参考代码
#include <cstdio>
#include <cctype>
#define int long long
const int N = 5e5 + 10;
struct Edge {int to, val, nxt;} e[N << 1];
int head[N], cnt, len[N], g[N], f[N], n, k, slen[N], pos[N], sz[N], maxson[N];
inline void AddEdge(int u, int v, int w) {
e[++cnt] = (Edge) {v, w, head[u]}, head[u] = cnt;
}
void dfs1(int u, int fa) {
if (pos[u]) sz[u] = 1;
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to, w = e[i].val;
if (v == fa) continue;
dfs1(v, u);
if (sz[v]) {
f[u] += (f[v] + 2 * w);
int now = len[v] + w;
if (now >= len[u]) slen[u] = len[u], len[u] = now, maxson[u] = v;
else if (now >= slen[u]) slen[u] = now;
}
sz[u] += sz[v];
}
}
void dfs2(int u, int fa) {
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to, w = e[i].val;
if (v == fa) continue;
if (!sz[v]) g[v] = g[u] + 2 * w, len[v] = len[u] + w;
else if (k - sz[v]) {
g[v] = g[u];
if (maxson[u] != v && len[v] < len[u] + w)
maxson[v] = u, slen[v] = len[v], len[v] = len[u] + w;
else if (len[v] < slen[u] + w) len[v] = slen[u] + w, maxson[v] = u;
else if (slen[v] < len[u] + w && maxson[u] != v) slen[v] = len[u] + w;
else if (slen[v] < slen[u] + w) slen[v] = slen[u] + w;
}
else g[v] = f[v];
dfs2(v, u);
}
}
inline int read(void) {
int x = 0, f = 1, ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) x = (x * 10) + (ch ^ 48);
return x * f;
}
void write(int x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x - (x / 10 * 10) + 48);
}
signed main(void) {
n = read(), k = read();
for (int i = 1, u, w, v; i < n; ++i)
u = read(), v = read(), w = read(), AddEdge(u, v, w), AddEdge(v, u, w);
for (int i = 1; i <= k; ++i) pos[read()] = 1;
dfs1(1, 0); g[1] = f[1]; dfs2(1, 0);
for (int i = 1; i <= n; ++i) write( g[i] - len[i] ), putchar('\n');
return 0;
}