前言
解析几何常常以其繁杂的计算而成为高考备考中的易错点与难点。解析几何虽然“解析”,但其本质还是“几何”,而巧妙发觉几何关系并利用向量等几何关系有时能极大简化运算。
下面让我们以向量的视角来看2024届浙江名校协作体高三下学期联考/九五名校联考(今年名协拉上了包括衡水,南京一中,华附,湖师附在内的全国多所名校一起)的解析几何题中的面积关系。
题目
已知过点 (1,0) 的直线与抛物线 E:y^2=2px\space(p>0) 交于 A,B 两点, O 为坐标原点,当直线 AB 垂直于 x 轴时, \triangle AOB 的面积为 \sqrt2 .
(1)求抛物线E的方程;
(2)若 O 为 \triangle ABC 的重心,直线 AC,BC 分别交 y 轴于点 M,N ,记 \triangle MCN,\space \triangle AOB 的面积分别为 S_1, S_2 ,求 \frac{S_1}{S_2} 的取值范围.
解答
第一小问
不妨 A 在 x 轴上方,则可以得到 S_{\triangle AOB}=\frac12\cdot1\cdot|AB| ,易得 A(1,\sqrt2) ,代入解得 p=1,E:y^2=2x .
第二小问
我们先把要求的图形画出来:
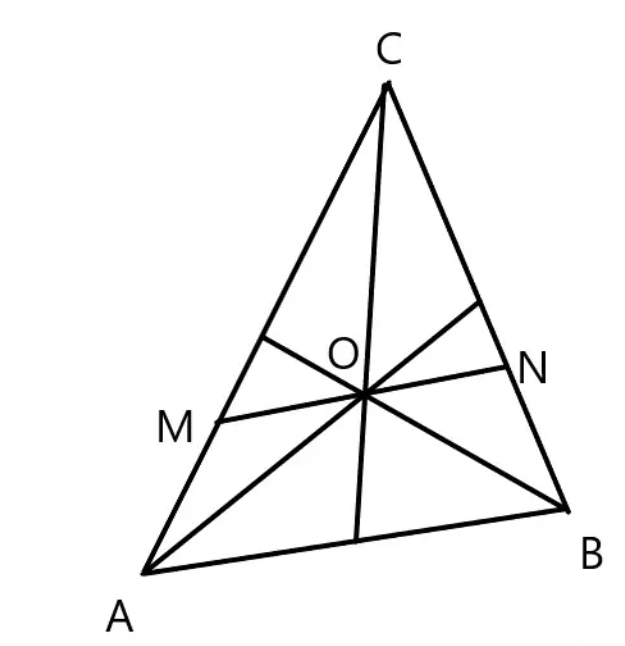
根据图形特征,我们选定 \vec {CA},\vec {CB} 为基底向量研究,
则由 O 为 \triangle ABC 的重心,得 \vec {CO}=\frac23\cdot\frac12\cdot(\vec {CA}+\vec {CB})=\frac13\vec {CA}+\frac13\vec {CB} ,
设 \vec {CM}=\lambda\vec {CA},\vec {CN}=\mu\vec {CB} ,则由 A,B 在 y 轴右侧,易得 \lambda,\mu\in(\frac12,1) ,由重心的性质, S_2=\frac13S_{\triangle ACB} ,故 \frac{S_1}{S_2}=3\cdot\frac{S_1}{S_{\triangle ACB}}=3\cdot\frac{|\vec{CM}|\cdot|\vec{CN}|\cdot sin\angle ACB}{|\vec{CA}|\cdot|\vec{CB}|\cdot sin\angle ACB}=3\lambda\mu ;
且 \vec {MO}=\vec {CO}-\vec {CM}=(\frac13-\lambda)\vec {CA}+\frac13\vec {CB} , \vec {NO}=\vec {CO}-\vec {CN}=\frac13\vec {CA}+(\frac13-\mu)\vec {CB} ,
由 M,O,N 三点共线,有 \vec {MO}=k\vec {NO} ,则 \frac13-\lambda=\frac13k,\frac13=(\frac13-\mu)k ,相除消去 k 并化简后得 \frac1\lambda+\frac1\mu=3 ,
故 \frac1{\lambda\mu}=\frac1\lambda(3-\frac1\lambda) , \frac1\lambda\in(1,2) ,故 \frac1{\lambda\mu}\in(2,\frac94],\lambda\mu\in[\frac49,\frac12) , \frac{S_1}{S_2}\in[\frac43,\frac32) .
这样,我们就从几何的视角,利用向量工具的强大力量解决了这道题目。
题目思考
自九省联考以来,解析几何命题的一个趋势就是“多想少算”,通过几何关系避开繁杂的代数运算,同时尽量让套路化解题方法不再有“秒杀”的效果。我们需要更多关注几何图形本身,并结合平面向量等工具,才能更快更准确地解决解析几何问题。
最后,祝大家在高考备考的路上有所收获,学习进步,共赴梦想!