写在前面
在高考备战中,函数与导数作为课标的重要组成部分,一直是高考和各类模拟考试的热点和难点。尤其是导数压轴题,以其高度的思维挑战性和技巧性,常常让考生感到困扰。对2023届重庆二模导数压轴题这种零点——极值点双变量问题,解题方法的选择更为重要,如果方法选择不当,就会导致过程的复杂化和计算量的增大,导致难以在规定时间内完成。在此类问题的解决中,较为恰当的策略就是将复杂的参数和变量分离出来,确定其取值范围,并利用函数的零点进行代换,从而巧妙地消除参数,简化问题。
下面,让我们来看看这道题目。
题目
(节选自2023届重庆二模)f(x)=ae^{-x}+\frac{lnx}x(a>0), x_0为f(x) 的零点, x_1为f(x) 的极值点,证明:lnx_1<{x_0}^2-x_0+1.
我们先来看看标答:

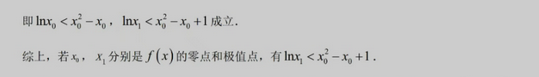
这么长的解答,还有这么复杂的函数构造求导,看着就头晕是不是?
但是,我们绝对不是没有更好方法!
条件转化与解答
根据题目,
为 的零点, x_0为f(x) 的零点, x_1为f(x) 的极值点,有
ae^{-x_0}+\frac{lnx_0}{x_0}=0①,
-ae^{-x_1}+\frac{1-lnx_1}{x_1^2} =0②
接下来,我们通过分离参数的方法,得到x_0和x_1的取值范围:
②变形得lnx_1=1-ax_1^2e^{-x_1},由于a>0 , :lnx_1<1 ,易得x_1<e,
①分离参数得a=-\frac{lnx_0\cdot e^{x_0}}{x_0},
由于a>0,所以显然 lnx_0<0,x_0<1
同时,我们观察目标式lnx_1<{x_0}^2-x_0+1,可以把对数消去,即为证明1-ax_1^2e^{-x_1}<{x_0}^2-x_0+1,即为{x_0}^2-x_0+ax_1^2e^{-x_1}>0
而由于a=-\frac{lnx_0\cdot e^{x_0}}{x_0},将其代入即为证明x_0^2-x_0>\frac{lnx_0\cdot e^{x_0}}{x_0}x_1^2e^{-x_1}这个仅含 x_0,x_1的不等式,那此时自然的思路是利用 x_0,x_1的大小关系实现放缩。
由题,ae^{-x_1}=\frac{1-lnx_1}{{x_1}^2},代入得 f(x_1)=\frac{1-lnx_1+x_1lnx_1}{{x_1}^2}=\frac{1+lnx_1(x_1-1)}{{x_1}^2},由lnx(x-1)\geq0得f(x_1)\geq\frac1{{x_1}^2}>0,x\to0,f(x)\to-\infty,由零点存在性定理,
x_0<x_1。
为实现放缩,我们还需要验证含x_1部分的单调性,才能实现消参:令g(x)=x^2e^{-x}求导得g'(x)=x(2-x)e^{-x},易得g(x)在(0,2)单增,在(2,e)单减,且g(e)=e^{2-e}>g(1)=e^{-1}
若x_1\leq2有 g(x_1)>g(x_0),2<x_1<e 有g(x_1)>g(e)>g(1)>g(x_0),
由于lnx_0<0,
\frac{lnx_0\cdot e^{x_0}}{x_0}x_1^2e^{-x_1}=\frac{lnx_0\cdot e^{x_0}}{x_0}g(x_1)<\frac{lnx_0\cdot e^{x_0}}{x_0}g(x_0)=\frac{lnx_0\cdot e^{x_0}}{x_0}x_0^2e^{-x_0}<0,
只需证明x_0^2-x_0>\frac{lnx_0\cdot e^{x_0}}{x_0}x_0^2e^{-x_0}即x_0-1-lnx_0>0,由熟知对数切线放缩显然成立,故得证。
解法分析
事实上在求解的过程中,我们的关键是将a消掉并利用x_0,x_1 的关系放缩,那我们就希望能找到最简的方法实现。通过对式子的观察,发现ax_1^2e^{-x_1} 将a代入后若将x_1 换为x_0,那绝大多数项都可以轻松消掉,再结合单调性分析和放缩实现替换的过程,那问题的最终解决就水到渠成了。
写在最后
在导数压轴题的求解过程中,仔细观察式子结构能够有效地简化解题过程,提高解题效率,让我们更轻松地应对数学难题。
最后,我们希望通过本文的介绍,能够激发大家对导数解题方法的探索和研究兴趣。数学是一门充满挑战和奥秘的学科,只有不断地探索和创新,我们才能更好地理解和掌握它的本质。在未来的学习和研究中,我们期待大家能够运用这一新方法,解决更多的数学问题,开拓更广阔的数学世界。
预祝大家元旦快乐!